Many newer models are evolving into towards "probabilistic" models, that is, models that take in to account that various outcomes.
In this article, I will discuss using two closely related mathematical functions that make useful (if limited, and limited to simple systems). They are the "y = ln(x)" and the "y = e^x" (aka y = exp(x) or "e to the x-power"). Much of this discussion is based in part from two of my earlier articles (http://robertmixblog.blogspot.com/2012/01/exponential-growth.html and http://robertmixblog.blogspot.com/2012/03/marginal-utility-and-gold.html).
***
I have "copied & pasted" the below, the heart of my "Exponential Growth" article. These graphs model inflation and growth of the US National Debt.
[clip]
All my graphs and comments below are not the exact numbers (which would be disputed anyway), but are close enough to make the lessons clear.
This first graph illustrates what happens in a constant 3% inflation from 1913 - 2012. 3% is close to the average rate of inflation since 1913, but is NOT the correct figure, but it is close enough. A hammer that cost $1.00 in 1913 would cost over $18.00 today, given that 3% inflation (blue series data points). The red data points show a 3 cent (not 3%!) fixed increase each year. I put the "red" data in because that would be what would have been PERCEIVED by a hammer buyer looking at a price change over a year or two (at least for the early years). CLICK on any of the graphs for a better view.
The next chart is "kind of the inverse (1/e^x, which I believe is also the "exponential distribution")" of the above and may be more familiar looking. It shows the value of the dollar falling vs. the 1913 dollar. Most researchers who have prepared a similar graph to the below usually arrive at a final end point of the 2012 dollar being only worth 3 cents. In my case here (using a constant 3% inflation), the dollar has fallen in value from 1913 - 2012 to about 4 - 5 cents:
This next graph extends the first graph out to the year 2032 (twenty years from now). You may be thinking two things:
1) 20 years, that's a long time. My response, look how the last 20 years have flown by...
2) That curve doesn't look so bad. My response, please look at the vertical scale, a $34 hammer in 2032 vs. $18 now...
The next graph is an extension out to 2062. Yes, I know that it is unlikely that we will see 3% constant inflation from now until then AND that 2062 is a year for our grandchildren, but it illustrates well what happens in "the out years" (note that the $1.00 1913 hammer is now over $80):
Let's play pretend one last time (or have a "Thought Experiment" for finicky adults who do not like to play). "Let's say" that in a moment of relative panic and seriousness that our politicians in 2017 (after Obama's second term or after Romney's first term) decide to get "really serious" about our debt. I mean it, really serious! And, let's say they are SO serious that they decide limit the growth of government debt by 5% per year (as the looming debt growing at 11% is starting to look scary even for politicians...). They are SO SERIOUS that they get a Constitutional Amendment through limiting growth of the debt to 5% a year! Wow! That's pretty serious! Well, that sounds pretty good, doesn't it? And 5% is not so much, no? Just a little bit over our projected economic growth rate. Hallelujah! Hallelujah!
Well, let's see:
[/clip]
***
The below is a similar clip from my "Marginal Utility And Gold" article. In that article I discuss "marginal utility", an economic term with how much you enjoy the next purchase of something that you enjoy, "units of happiness or satisfaction" if you will.
[clip]
From Wikipedia, the free encyclopedia
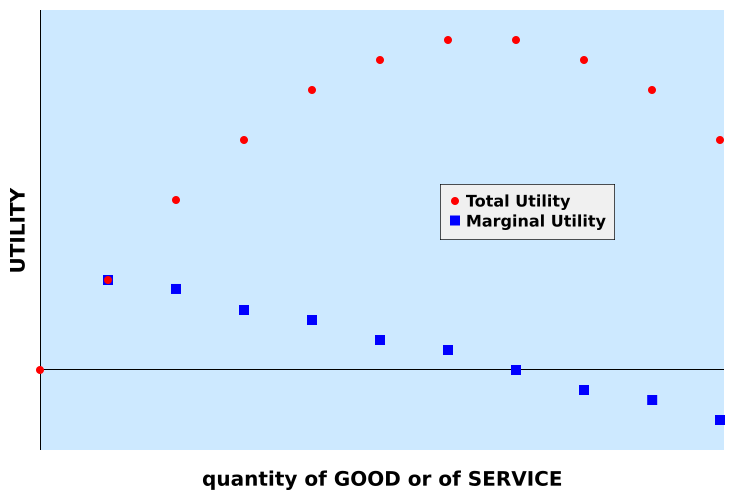
Let's do one of my beloved "Thought Experiments" here to explore this graph. "Let's say" you are the head of a happy household with FIVE CHILDREN (are you reading this Amy?), and let's also say that you just won a decent amount of money from your local lottery (say $1,000,000 free and clear, in cash now, taxes already paid). Let's also assume that you are middle class, not deep in debt and have your retirement money put aside OK. So, you are free to spend the money!
You determine that your major purchases are to be to upgrade your transportation, you deserve it, so why not? So, before you head out the door, you are at the very beginning of the above graph. You decide to buy a BMW! Wow, that felt good, didn't it? You are now at that next point on the graph, shared by the blue square and the red dot. The Y-axis is your "utility", how good you feel being a BMW owner. You got a nice chunk of utility from buying the car. So, you decide to buy your wife as well! Smart move, she is likely to be very happy too. Now, take a close look at the graph to see WHAT it is charting. The red dots are your TOTAL happiness (utility) from buying the two (for now) cars. The blue squares show your marginal utility, that is how much EXTRA pleasure you got from your most recent purchase. You will note you got almost as much pleasure from buying that second car as from the first. That is still pretty good though.
You then decide that your oldest child gets to have a BMW as well, s/he's a good kid, right? So you buy BMW number three. But, to be fair, you decide to buy EACH one of your children in turn a new BMW. At this point, you are probably not getting any extra happiness from that seventh car! And THAT is where the blue square is there at zero (no extra happiness) and the red dots are as high as they are going to go. Let's say you buy yet another BMW... You will likely NOT derive any utility here, in fact, if this Thought Experiment follows this graph, you would LOSE utility (be LESS happy) because where are you going to park that eighth car...?
Most products and services are like this. If you like Big Macs, that first one is yummy! The second will likely fill you up, that is likely to be as much as you want (maximum utility). The third Big Mac would likely make you sick...
***
But, gold is different. I mentioned near the very top of this article that I responded to two new buyers of precious metals. I told them both that AT LEAST FOUR TIMES that I had reached a convenient "round number" of ounces of gold that I wanted to hold, and that would be that. I would not need anymore. But, soon thereafter, I found that, well yes, that I could buy just a little bit more gold.
In other words, at least four times I thought that I would have enough gold to keep me happy only to find I wanted more...
So, gold would NOT follow the above graph from wikipedia. My best guess is that gold would follow a path similar to the "y = ln(x)" curve. Where the Y-axis is total utility and the X-axis increasing gold ownership through time. The ln(x) curve is the INVERSE of the exponential curve (the e^x, "e to the x power"). There are two graphs below, the first one is ln(x) up to 500 oz of gold owned and showing a "utility" of about 6.1. The second graph shows ln(x) out to 5000 ounces, with a utility of about 8.2.
Three quick notes about the above two graphs. The first is that I put in "Y-axis" values below zero because that is the actual way the ln(x) curve is. Secondly, note each unit of "utility" is worth a LOT (5000 oz of gold is approximately 206 lbs of gold, troy ounces remember)! Third, take a good look at the SHAPE of the two curves, they are essentially identical! They scale exactly the same, just like the more well known exponential curve. If I am interpreting this right, marginal utility of increased gold holdings scales very nicely all the way up the curve!
[/clip]
***
I mentioned up there in the exponential growth part that the inverse of e^x is the 1/e^x, the traditional way that we non-math majors think of the inverse ("one over (the function)").
There is another way to think about y = e^x and y = ln(x) however. These two functions are the inverse of each other in another way. They are mirror images of each other about the "y = x line". See below graph:
The blue diamonds above are "y = exp(x)", the red squares are "y = ln(x)" and the green triangles are "y = x". Note that ln(x) and exp(x) do indeed mirror-image each other off of the "y = x" line. Pick a convenient value of y or x (say 15), and note that the distance from (15,15) to each curve is the same (I leave proof of this as an exercise for the reader).
The exponential function is well known for modeling many phenomena. I have to think that its inverse, the natural logarithm should model some things we see as well.
***
Here is a blog link to a guy writing on kind-of similar pieces as the above. It is worth your while to take a look:
https://pearlsforswine.wordpress.com/
Exponential growth is a very important topic of mathematics as its has immense use in research work.
ReplyDeleteexponential growth